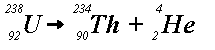
Suppose we have a radioactive decay process of the general form

This means that each atom of the radioactive substance A breaks down into a collection of smaller atoms and/or subatomic particles. Phenomena as diverse as dating ancient artifacts and assessing the dangers of nuclear wastes depend on knowing the rate of decay for such reactions.

Here are two examples of specific radioactive decay processes:

(a)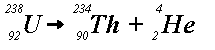 

(b)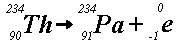
In both cases, the notation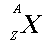means X is the chemical symbol for the element, A is the number of nucleons (protons and neutrons), and Z is the number of protons. Example (a) indicates that uranium-238 releases an alpha particle (i.e., a helium nucleus) to produce thorium-234. This is called alpha-decay. Example (b) shows that thorium-234 releases a beta particle (i.e., an electron) to produce protactinium-234. This is called beta-decay. Unstable nuclides, such as uranium-238, start series of disintegrations that continue until a stable nucleus results. Mass is lost in both alpha and beta decay processes. This mass is converted into energy: radiation.

In 1903, Rutherford and Soddy, in a paper entitled Radioactive Change, proposed the law of radioactive change. They observed, in every case they investigated, that the rate of decay of radioactive matter was proportional to the amount present. If we write (as chemists do) [A] for the concentration of the substance A, then the law of radioactive change becomes

The value of k is called the decay constant for A.

This law can be justified in the following way: For any fixed time interval, there is a certain probability (a number r between 0 and 1) that each atom of the radioactive substance will disintegrate. Thus, during this time interval, we should expect that the number of atoms that actually do disintegrate is r times the number present at the start of the interval. That's equivalent to saying that the rate of change of [A] is proportional to the amount present.

We will discuss this "rate of change" relationship in much greater detail later.  Nevertheless, the functions that have rate of change proportional to the amount present (exponential functions) have the form
 

for some base b, where y₀ is the starting amount. Thus, we would expect that a concentration function for a radioactive substance has the form
 

where b is a number between 0 and 1 (in order to have decay rather than growth), and [A]₀ is the starting concentration.

There are several quantitative aspects of radioactivity that are important for managing nuclear waste materials, including how much radioactivity a given substance emits, how concentrated the substance is in its surrounding medium, how dangerous its emissions are to human and other biological populations, and how long the substance goes on being radioactive. In this module we will address only the last of these issues, the time that a given substance remains dangerous.

• Using either the "rate of change" concept or the equation above for [A](t), explain why the function [A] must have a constant time to reach half the original concentration, no matter what the starting concentration is (one possible explanation would be to indicate how this time is found).  The constant time for halving concentration is called the half-life of the substance, and is denoted T_1/2.

Part 2: Rapid Decay

In order to determine a half-life directly from obervational data, the radioactive substance must decay rapidly enough that one can actually measure a change. Not surprisingly, the earliest radioactive substances studied were ones that decayed fairly rapidly. The data in the following table are from a paper published by Meyer and von Schweidler in 1905. Their numbers are not concentrations but rather measurements of "relative activity." Since the rate of radioactive emission is proportional to the amount present, one can measure amounts (relative to the starting amount) by observing instead the emission rates (relative to the starting rate).
 

Source: S. Meyer and E. von Schweidler, Sitzungberichte der Akademie der Wissenschaften zu Wien, Mathematisch-Naturwissenschaftliche Classe, p. 1202 (Table 5), 1905, as reported in J. Tukey, Exploratory Data Analysis, Addison-Wesley, 1977.

1. Enter the data points in your calculator, and plot them. Does the decay pattern look roughly exponential -- that is, of the form


y = y₀b^t,

with b < 1? If so, can you determine either y₀ or b directly from either the graph or the data table?

2. Enter a new list in your calculator corresponding to log(relative activity), and plot log(relative activity) vs. (time).  (Ask if you do not know how to do this easily.)  Does this plot confirm or deny an exponential form for the data? Explain why using the algebra of exponentials and logs (hint: take the log of both sides in the above equation).
3. Use the plot to estimate the coefficients m and c for a line of the form


Y = mx + c

that appears to fit the data in this plot.  (You may use the calculator to find the "best fit" line, but do the estimate first.  The calculator will use the symbols Y=ax+b, but the number b may of course be different from the "b" in the exponential formula above.)

4. From your coefficients m and c, find a function of the form
y = y₀b^t

(it is possible to get the calculator to do this automatically, but show the algebra for doing the calculation using your m and b) that should fit the data points well. Plot this function together with the data.

Part 3: The Half-Life

1. Use your model function (the formula) from Part 2 to estimate the half-life T_1/2 of the radioactive substance studied by Meyer and von Schweidler. (For simplicity of notation, we will refer to this quantity as T.) Discuss the reasonableness of your answer in light of the data. How many halvings take place in the time frame of the observations?
2. Another way to write the same model function is


y = y₀ 2^-t/T.

(Can you explain why?)  That is, decay functions can be expressed as exponentials with base 2 by scaling time by the half-life.

Answer each of the following questions in your worksheet.

1. Why do we expect a model function for the amount (or concentration) of a radioactive substance to be an exponential function?
2. Given data from a presumably radioactive substance, how can we tell if the data decay exponentially?
3. Describe the key steps in finding a model exponential function to fit decay data.
4. Once we have the model function, how do we find the half-life?
5. Is it preferable to find a half-life directly from the data or from the model function? Explain your conclusion.

Why do we measure the duration of radioactivity in half-lives instead of lifetimes?
 
 
 

This lab has been adapted from materials developed by William Barker, Bowdoin  College, and David Smith, Duke University for the  Connected Curriculum Project with funding from the National Science  Foundation.  Used by permission.