A continued fraction is a particularly elegant representation of rationals related to the Euclidean algorithm, of the form
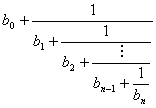 , where each bi
is a positive integer. In the case of reals, the fraction continues
indefinitely. A bounded continued fraction is one in which each of
the bi's has
some maximum value. It has been proven that any real can be represented
as the sum of two bounded continued fractions, with maximum value four.
Unfortunately, the method is not applicable to rationals, and we
don’t know whether every rational can be represented as the sum
of two finite bounded continued fractions. The aim of this project is
to numerical investigate how hard it is to represent an arbitrary
rational by bounded continued fractions.
, where each bi
is a positive integer. In the case of reals, the fraction continues
indefinitely. A bounded continued fraction is one in which each of
the bi's has
some maximum value. It has been proven that any real can be represented
as the sum of two bounded continued fractions, with maximum value four.
Unfortunately, the method is not applicable to rationals, and we
don’t know whether every rational can be represented as the sum
of two finite bounded continued fractions. The aim of this project is
to numerical investigate how hard it is to represent an arbitrary
rational by bounded continued fractions.The kissing problem asks how many spheres can touch a central sphere without overlapping in n-dimensions. The solution is known for dimensions two to four, and there are bounds on the solution in higher dimensions. The aim of this project is to try and improve upon these bounds using a numerical optimization algorithm I have developed to distribute spheres.
The logistic equation
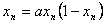 is a classic example used to explain bifurcation and the onset of chaos. However, it is assumed that x
is a real variable. The logistic equation was originally derived as an
iteration on populations, and hence integer values. The aim of this
project is to investigate the effect of assuming integer solutions only
for the equivalent population model. Do we still see period doubling to
chaos in the same way?
is a classic example used to explain bifurcation and the onset of chaos. However, it is assumed that x
is a real variable. The logistic equation was originally derived as an
iteration on populations, and hence integer values. The aim of this
project is to investigate the effect of assuming integer solutions only
for the equivalent population model. Do we still see period doubling to
chaos in the same way?Dreidel is a simple game played during Hannukah, which previous publications have proven to be unfair. Unfortunately, these results were flawed because they assumed winnings could be arbitrary reals. Using a Markov chain approach, we can work out probabilities exactly. So what are your chances of actually winning Dreidel?
A circle pack is a collection of circles with a given set of tangencies. The (unique) radius of each circle can be found given the radius of boundary circles, and leads to a variety of efficient algorithms. But what if the radii given are not for all the boundary circles? We will develop some new algorithms for the circle pack problem, and use them to try and find conditions on the initial radii that guarantee a circle pack is unique.
A convex hull is the smallest convex polygon that completely encloses a set of points. Previously, I have had an undergraduate research student do a project comparing the efficiency of various algorithms to find the convex hull of points in the plane. The aim of this project would be to extend the previous work by looking at more algorithms, and seeing how they compare.
We all know about solving Sudoku's by now, but how hard is it to find an initial set-up with a unique solution? The aim of this project is to build an effficient Sudolu solver, then use it to investigate the distribution of how many solutions there are for initial set-ups with various conditions.
A transitive relationship says that if A betas B and B beats C, then A must beat C. In a non-transitive situation, C beats A. Several examples of non-transitive dice are known, where the aim is to get the larger score when rolling: the first set beats the second, which beats the third which beats the first. The aim of this project will be to examine whether other nontransitive dice sets are possible, and what conditions are required for nontransitive sets.
The Goldbach conjecture is one of the more famous unsolved problems in number theory: can every even integer be represented as the sum of two primes. What is less known is that it appears that all but 33 even integers can be represented as the sum of two twin primes, primes that differ by two. The aim of this project will be to investigate the number of representations of even integers using twin primes, and see if there are smaller sets that appear to have the same properties.