COURSE GUIDELINES
Math/Physics 365-Computational Fluid Dynamics-Spring 2000
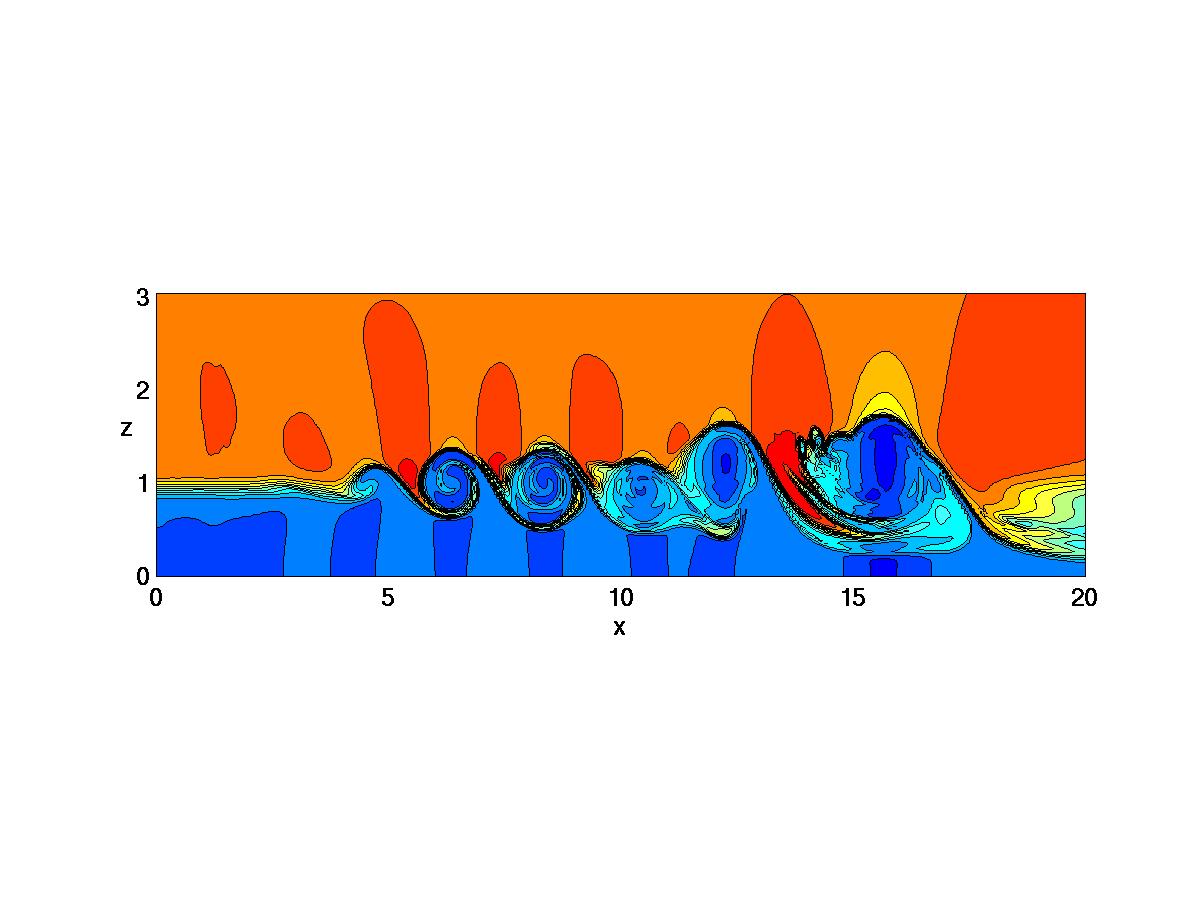
FIG1: [STILL image] Contours of constant
density in heated subsonic (Mach 0.8) round jet. Flow is left to right
with jet axis along lower
boundary. (Pruett, AIAA Journal, to appear.)
OVERVIEW: The motion
of fluids holds both aesthetic and practical fascination for humans. The
science of fluid mechanics provides insight into phenomena as diverse as
wave action, ocean circulation, weather patterns, the destructive power
of tornados and hurricanes, the science of flight, shock waves, the droplet
pattern in a half-empty wine glass, the laminar-turbulent transition of
a smoke plume rising from a cigarette, blood flow in the heart, and the
accretion of galaxies. Because of the complicated nature of the Navier-Stokes
equations that govern fluid motions, prior to the second half of the 20th
Century, fluid dynamicists could rely only upon simplified theories corroborated
by physical experiments to explain and predict fluid-flow phenomena. With
the advent of the digital computer, numerical simulation joined theory
and experiment in the arsenal of scientific techniques that can be brought
to bear in unraveling the mysteries of fluid flow. To date, the quest for
a virtual wind tunnel to replace the physical wind tunnel has been somewhat
illusory. Nevertheless, with continuing advancements in both computer technology
and algorithmic efficiency, computational fluid dynamics has emerged as
a powerful and (in the right hands) trustworthy tool for the design of
spacecraft, aircraft, and automobiles. In the future, numerical simulation
will become ever more important as an emerging "key technology." Say the
authors of our text: "The numerical simulation of physical phenomena requires
the observations and models of the natural scientist, the technical expertise
of the engineer, the numerical methods of the mathematician, and the modern
techniques and computers of the computer scientist." This course has been
specifically designed as an integral part of JMU?s and NCCU?s collaborative
NSF-funded computational-science
track to help you--the student--develop and hone the triad of skills
that comprise a solid foundation in computational science: modeling
of physical phenomena, numerical methods, and scientific visualization.
PREREQUISITES: Math
237, Math 238 (formerly 301E), Math/Phys. 265, and Phys. 340
INSTRUCTORS:
| Dave Pruett |
|
|
|
| Dorn Peterson |
|
|
|
| Jim Sochacki |
|
|
|
PRIMARY TEXT: Numerical
Simulation in Fluid Dynamics: A Practical Introduction by Michael Griebel,
Thomas Dornseifter, and Tilman Neunhoeffer, SIAM 1998.
TECHNOLOGY: Proficiency
in a high-level programming language such as Fortran 90 or C is expected.
Familiarity with computer algebra systems (CAS) such as Matlab, Maple,
or Mathematica would be helpful.
GRADING:
|
|
|
| 20% Midterm exam | TBD |
| 10% Homework/Lab. assignments | Selected HW/Lab. assignments to be graded |
| 50% Programming assignments | 5-6 during semester/may include presentations |
| 20% Final exam | TBD |
OUTSIDE HELP: First
instructor's (Dave Pruett's) office hours: TBD and by appointment. During
scheduled hours, no appointment is necessary; outside of these hours, the
favor of an appointment is requested.
ATTENDANCE POLICY: Individual
success and the success of the course will require faithful on-time attendance.
LATE POLICY: No
credit will be given for assigments turned in after the due date
unless an extension period has been negotiated with the instructor at
the time the assignment is made.
HONOR POLICY: Students
are presumed to have high standards of integrity. To reinforce these standards,
the JMU Honor Code will be strictly enforced.