A classic question of plane geometry asks for the greatest area that can be enclosed by a figure of a given perimeter. This is known as the isoperimetric problem, and it has a pedigree going back to the ancient Greeks. A more modern formulation begins with an n-dimensional manifold and considers the set of all (n-1)-dimensional hypersurfaces that divide the manifold into two pieces. For each such hypersurface we compute the ratio of the area of the surface to the volume of the smaller of the two pieces, and we seek the infimum of the set of such ratios. In 1970, Jeff Cheeger proved that the first eigenvalue of the Laplacian of the manifold can be bounded below in terms of this infimum, now called the Cheeger constant in his honor.
In 1982, Peter Buser established that the eigenvalue spectrum of the manifold could also be bounded above in terms of the Cheeger constant. Buser then introduced a combinatorial analog of the Cheeger constant that applies to finite, simple graphs. This analog is called the isoperimetric number and is defined as follows: We take a finite simple graph and consider its edge-cutsets. We then seek the cutset that minimizes the ratio of the number of edges in the set to the number of vertices in the smaller of the two pieces. This minimal ratio is the isoperimetric number of the graph. Since a graph is a sort of degenerate manifold, it is not surprising that the isoperimetric number is related to the eigenvalues of the graph.
Buser developed the isoperimetric number as a tool for studying spectral geometry; the idea was to gain information regarding the spectrum of a manifold based on properties of certain associated graphs. However, his creation is now of independent interest to combinatorialists.
My PhD thesis considered certain families of Cayley graphs associated to the matrix groups PSL(2, Zn). I derived strong upper and lower bounds on the isoperimetric numbers of these graphs. These particular graphs are interesting because they arise in a natural way from arithmetic Riemann surfaces. More specifically, we know that the modular group acts on the complex upper half plane via fractional linear transformations. The standard fundamental domain for this action is known as a modular triangle. If we consider instead a congruence subgroup of the modular group, then a fundamental domain is obtained by gluing together, along boundary edges, an appropriate collection of modular triangles. After certain edges are identified, the result is a Riemann surface. The graphs obtained by associating a vertex to each triangle and connecting vertices that represent adjacent triangles, are precisely the aforementioned Cayley graphs. In my thesis, I exhibited an explicit action of the modular group on these surfaces, and then used this action to demonstrate the graph isomorphism. This work was published in the two papers: “Isoperimetric Numbers of Cayley Graphs Arising From Generalized Dihedral Groups,” and “Constructing Cayley Graphs Via Tesselations of Riemann Surfaces.”
After leaving graduate school, I spent three years at Kansas State University. There I met my long-time research collaborator Dominic Lanphier. Our first paper, “Cheeger Constants of Platonic Graphs,'' established a major generalization of prior results due to Brooks, Perry and Petersen. We did this by proving a novel decomposition theorem for Cayley graphs of matrix groups. In a second paper, ``A Decomposition Theorem for Cayley Graphs of Picard Group Quotients,'' we showed that our decomposition technique could be applied to other families of Cayley graphs.
Since the Cheeger constant is defined as an infimum, upper bounds are, in principle, easy to come by. Any explicit cut-set will produce an upper bound. Lower bounds are trickier, however. A well-known technique was to apply certain counting arguments to highly-connected graphs, to show that some minimum number of edges had to be cut to isolate a set of a given size. By using techniques from the theory of iterated functions, we were able to sharpen this method. We then applied our refinements to obtain significant improvements in the known lower bounds on the Cheeger constants of our Cayley graphs. This work was published in the paper “Lower Bounds on the Cheeger Constants of Highly Connected Regular Graphs.”
At this time we realized that our general approach ought to work for Levi Graphs as well, by which we mean graphs that arise in a natural way from certain combinatorial designs. In the summer of 2005 I gave this problem to undergraduate students Chris Miller and Amber Russell, who were working with me in a summer REU program. They successfully worked out the considerable details, and this work was published in the paper, “Expansion Properties of Levi Graphs.”
In two subsequent papers, we extended our techniques into new domains. In “Cheeger Constants of Arithmetic Hyperbolic 3-Manifolds,” we obtained improved, computable bounds on the Cheeger constants of these manifolds, and therefore also bounds on the first eigenvalue of the Laplacian. By adapting probabilistic methods due to Brooks and Zuk, we were able to obtain sharper, asymptotic bounds. Most recently, we were able to improve the known bounds for random, regular graphs of high degree, and for Platonic graphs over the rings Zn. This work was published in the paper, “Isoperimetric Numbers of Regular Graphs of High Degree With Applications to Arithmetic Riemann Surfaces.”

In 2007, a chance meeting with an editor from Oxford University Press led to the publication of my first book, The Monty Hall Problem: The Remarkable Story of Math's Most Conentious Brainteaser. The theme is that an entire course in probability theory can be taught with nothing more than variations of the Monty Hall Problem.
Though I had not planned on this becoming a new scholarly interest of mine, that is how things ended up. In 2011, my second book, coauthored with Laura Taalman, was published, again by Oxford University Press. It was entitled Taking Sudoku Seriously: The Math Behind the World's Most Popular Pencil Puzzle. The book was directed in part to students and mathematically interested lay people, and showed how natural questions that a mathematician would instinctively ask lead naturally to sophisticated ideas in combinatorics, algebra and number theory. This book won the 2012 PROSE award from the Association of American Publishers, for the best book of the year in popular science or mathematics.
Recreational mathematics has not always been taken seriously as a legitimate research area. That changed with the inauguration of the MOVES conferences, hosted by the Museum of Mathematics in New York. "MOVES" stands for the "Mathematics of Various Entertaining Subjects." The point of the conferences was that significant mathematics can arise from work on recreational topics. Together with my friend Jennifer Beineke, I edited three books of peer-reviewed proceedings for this conference, between 2015 and 2019, published by Princeton University Press. We published papers from luminaries like John Conway, Richard Guy, Peter Winkler, Erik Demaine, Tonya Khovanova, Persi Diaconis, and Ron Graham, as well as numerous other talented writers.
More recently, I have become interested in logic and logic puzzles. My
book Games for Your Mind: The History and Future of Logic Puzzles,
was published by Princeton University Press in November 2020. The book tells the history
of logic through the use of puzzles and brainteasers. It especially focuses on
the work of Lewis Carroll and Raymond Smullyan. Additionally, I explore the
possibilities of devising puzzles based on non-classical logics. I have
also published two papers about non-classical logic puzzles: "Non-Classical Knights and
Knaves" and "Knights, Knaves, Normals, and Neutrals."

I mentioned that my position at Kansas State University involved issues in mathematics education. As a result, I took a professional interest in anything related to public education. At that time, the Kansas State Board of Education had made national news by eliminating topics such as evolution and the Big Bang from the state's high school science standards. I was there right when that issue was coming to a head.
Shortly after moving to Kansas, I attended a conference for religious home-schoolers. To my surprise, all of the keynote speakers were from an outfit called “Answers in Genesis,” which promoted young-Earth creationism. That is, they believed that the Earth was no more than several thousand years old, and that the Biblical accounts of Adam and Eve and Noah's flood were historically accurate. This was my introduction to the issues surrounding evolution and creationism.
As I learned more about this issue, I was surprised to find that creationists, and the closely allied intelligent design (ID) proponents, frequently used superficially sophisticated mathematics in making their arguments. These arguments were drawn from probability theory, information theory, combinatorial optimization, and thermodynamics. These arguments were often proffered by well-credientialed people, and it could be difficult for lay people to see through their many flaws. I found it troubling that mathematics was being employed in the service of a an anti-scientific religious agenda, and that is why I began writing about this topic.

My first serious piece of writing in this area was a lengthy letter to the editor published in The Mathematical Intelligencer, entitled “How Anti-Evolutionists Abuse Mathematics.” It was a reply to a pro-ID editorial published in the magazine. Shortly thereafter, the reputable academic publisher Rowman and Littlefield published an ID book called No Free Lunch, the reference being to a famous collection of theorems from the theory of combinatorial optimization. The book's author was a mathematician who claimed that the modern theory of evolution could be refuted mathematically. I was subsequently invited to review the book for the academic journal Evolution, and my essay was published under the title, “Probability, Optimization Theory, and Evolution.”
Since one of the main problems in this area is the frequently misleading coverage in the media, I teamed up with Glenn Branch of the National Center for Science Education to write the article “Media Coveraqe of “Intelligent Design”, published in BioScience magazine (which is roughly comparable to the American Mathematical Monthly).
While I find the arguments of anti-evolutionists entirely unpersuasive scientifically, and while I
frequently deplore the tactics used by the movement's leaders, I had quite a different experience
when circulating among rank-and-file creationists. Starting in Kansas, and continuing after my move
to Virginia, I frequently attended creationist conferences and other gatherings. Sometimes these were
large, national conventions, while other times they were small gatherings at local churches.
Over several years I attended a few dozen of these gatherings. Based on that experience, I came
to feel that much of the academic writing in this area misrepresented who creationists were and
why they believed the things they did. Consequently, I wrote my book Among the Creationists:
Dispatches From the Anti-Evolution Front Line, published by Oxford University Press in 2012.
This book was a departure for me, in that it was more sociology than math or science. However,
I remain very proud of it. The stereotype of the ivory tower academic has merit, and it is
important for mathematicians and scientists to take an interest when their disciplines are
being used for nefarious ends.
After receiving my PhD in 2000, I began a post-doctoral position at Kansas State University. This position involved curricular development issues in mathematics education, and was not directly relevant to my research. There was no one at the university with comparable research interests to mine. However, since there were number theoretic aspects to my thesis work, I started participating in the number theory seminar. This led to my collaboration with Todd Cochrane and Christopher Pinner, involving certain problems about exponential sums.
The study of exponential sums has a long history in number theory. Gauss used them to prove the law of quadratic reciprocity, and his techniques were later used by other mathematicians to prove higher order reciprocity laws. The circle method of Hardy, Littlewood and Ramanujan leads naturally to a consideration of exponential sums when applied to Waring's problem. These are just two examples, among many, of the importance of exponential sums.
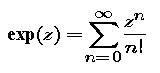
By an exponential sum we mean a finite sum whose summands are all found on the complex unit circle. The goal is to find upper and lower bounds on these sums, a task to which mathematicians have applied considerable intellectual firepower over the years. Keeping up with the state of the art can be a daunting task, as ever more sophisticated techniques are invoked to make ever more marginal improvements in existing bounds.
Our work focused on polynomial exponential sums, by which we mean sums of the form exp(2πif(x)/p), indexed over a complete residue system for p. We assume the polynomial f(x) has integer coefficients. “Waring's problem mod p” refers to the problem of finding the smallest value of k such that for any positive integer N, we can find k integers whose function values sum to something congruent to N mod p. In our first paper, ``Bounds on Exponential Sums and the Polynomial Waring Problem Mod p,'' we generalized to arbitrary polynomials results of Konyagin that were valid only for monomials. Such bounds lead in a natural way to bounds on the polynomial Waring's problem mod p.
The bound we proved as our main result in this paper had the number of terms in the polynomial as one of its variables. When this parameter was small, sharper bounds could be obtained. In our second paper, ``Sparse Polynomial Exponential Sums,'' we used the main result of our first paper to sharpen the known upper bounds in the special case of a “sparse” polynomial. By this we mean a polynomial with a small number of terms relative to its degree.