with the constraint that ![]() .
Solving the constraint for
.
Solving the constraint for ![]() , we get
, we get
![]() , and thus
, and thus
Differentiating with respect to ![]() , we get
, we get
which does not exist when ![]() , and is zero when
, and is zero when ![]() , i.e.
when
, i.e.
when

For this ![]() we have
we have
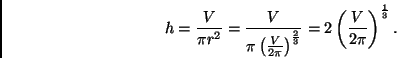
Therefore, the ratio of height to radius must be
![]() ,
regardless of the desired volume
,
regardless of the desired volume ![]() of the can.
of the can.