Problem of the Week #10

Spring 2006: Special All-Sudoku Semester

This week's puzzle has additional regions that are ordered. Each "worm" region contains distinct integers that either increase or decrease from one end to the other (although NOT necessarily sequentially); this can place very strict restrictions on parts of the puzzle. For example, consider the "worm" in the upper right corner of the puzzle. Clearly the entries in this worm must increase from the "3" (there aren't enough positive integers less than 3 for it to decrease). This means that the cell directly beneath the 3 can only be one of 4, 5, or 6. We stop at "6" because that is the largest number that will allow us to fill in the rest of the worm in an increasing way.

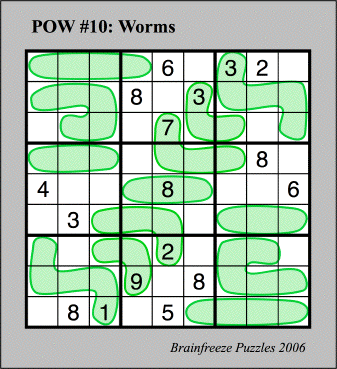
Rules: Fill in the grid with the numbers 1, 2, 3, 4, 5, 6, 7, 8, and 9 so that each row, column, and block has no repeated entries, and so that in addition each shaded "worm" contains numbers in strictly increasing or strictly decreasing order from one end to the other.

For any Sudoku variation puzzle that consists of a regular Sudoku puzzle with additional restrictions or conditions, the first question we should ask is whether or not the puzzle would be solvable as a regular Sudoku puzzle, without the extra conditions. For example, is the puzzle above solvable without taking into account the "worm" conditions? Of course just "not being able to figure it out" is not a proof that the puzzle is not solvable without the worms! In this particular example there is an easy way to tell that the worms are necessary -- that is, provided that you believe a conjecture from the first Problem of the Week from this semseter.

Solutions are due by noon on Tuesday, March 28, 2006.
Return solutions ON PAPER to Laura Taalman, Burruss 127, MSC 7803.
Include your name and email address with your solution.