Problem of the Week #14

Spring 2006: Special All-Sudoku Semester

This is the last problem in our All-Sudoku Semester! Last week's Clock Sudoku puzzle knocked a lot of people for a loop. This week the puzzle is another "throw-out-all-the-rules" variation, but not quite as difficult. By using hexagons instead of squares for our Sudoku cells, we can make a puzzle that has three types of "linear" regions (rows, increasing columns, and decreasing columns) instead of the usual two (rows and columns on a regular Sudoku board). Notice that many of the rows and "columns" have less than 10 cells and therefore are not full Sudoku regions (although we do require that they contain no repeated entries).

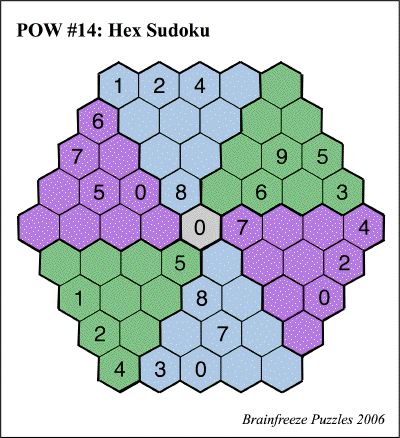
Rules: Fill in with the integers 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 so that there are no repeated entries in any row, in any increasing column, or in any decreasing column, and in addition there are no repeated entries in any of the six shaded triangular regions.

The only regular polygons that tesselate or tile the plane are triangles, squares, and hexagons, so a hexagon-celled Sudoku board is a natural alternative to the usual square grid. What about a Sudoku board with triangular cells? What configurations of hexagons or triangles have possible/fun Sudoku games? Do interesting variations arise if we consider a tesselation with pairs of regular polygons (like octagons and squares)?

Stay tuned for the date and time of the POW/Sudoku party during the last week of school!
There will be door prizes and a Sudoku game/contest. Students and faculty who have completed all (or all but one) of the Problems of the Week will also be eligible for special awards.

Solutions are due by noon on Tuesday, April 25, 2006.
Return solutions ON PAPER to Laura Taalman, Burruss 127, MSC 7803.
Include your name and email address with your solution.