Problem of the Week #2
Spring 2006:
Special All-Sudoku Semester
We hope you enjoyed last week's basic Sudoku puzzle, since that was the
last "normal" Sudoku puzzle of the semester.
This week's variant on Sudoku is simply to have a larger board. Regular
Sudoku has a 9 x 9 board divided into 3 x 3 blocks.
Notice that
the number of cells in each row and column are equal to the number
of cells in each of the blocks. The next largest size board that allows
this is a 16 x 16 board: because 16 is a perfect square, we can divide
a 16 x 16 board into 4 x 4 blocks (with 16 entries each). Boards of
this size sometimes appear under the name "Super Sudoku". For 16 x 16
Sudoku, we will need 16 different symbols; perhaps the math-geekiest choice
of 16 symbols is the set of 16 one-digit hexadecimal numbers:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
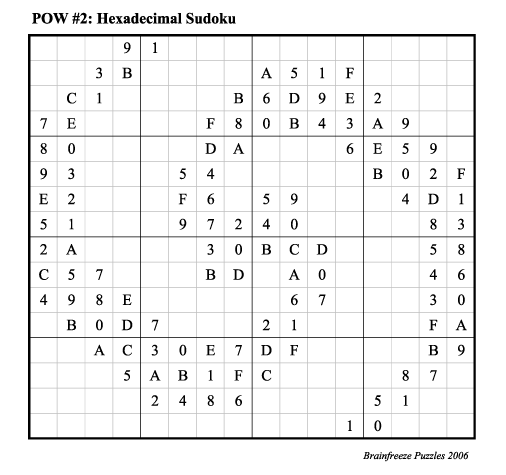
Rules: Fill in the grid below
so that each row, each column, and each of the sixteen 4 x 4 blocks contain
all of the one-digit hexadecimal numbers exactly once.
Open question:
Last week we mentioned that the number of 9 x 9 Sudoku boards is known.
It is not known how many 16 x 16 Sudoku boards are possible.
Can you figure it out?
Solutions are due by noon on Tuesday, January 24, 2006.
Return solutions ON PAPER to Laura Taalman, Burruss 127, MSC 7803.
Include your name and email address with your solution.

