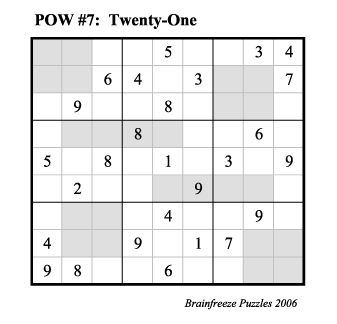
Rules: Fill in the grid below so that each row, each column, and each 3 x 3 block contains the integers 1, 2, 3, 4, 5, 6, 8, and 9 exactly one, with the added condition that the six shaded regions have entries that sum to 21. Each shaded region must contain distint entries.

Like last week's "Magic Squares" puzzle, this week's puzzle involves sums. This allows us to ask a larger variety of questions than we could ask about other Sudoku variations (whih usually use numbers as placeholders only, with no numerical value). For example: What types of regions can be "21" regions as part of a Sudoku board? What is the maximum number of "21" regions that can be put into a Sudoku board? What is the minimum number of initial conditions that will lead to a unique solution, given that the maximum number of "21" regions is used? Are there Sudoku boards with no "21" regions at all? What if a number other than 21 is used?
Solutions are due by noon on Tuesday, February 28, 2006.
Return solutions ON PAPER to Laura Taalman, Burruss 127, MSC 7803.
Include your name and email address with your solution.