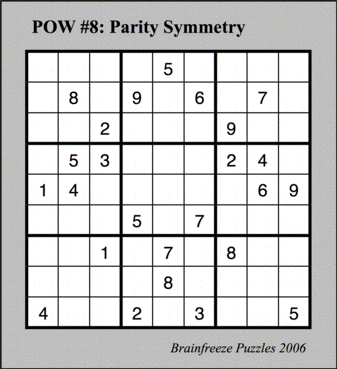
Rules: Fill in the grid so that each row, each column, and each 3 x 3 block contains the integers 1, 2, 3, 4, 5, 6, 7, 8, and 9 exactly once, with the additional condition that in the completed puzzle, the set of cells containing even numbers has 180 degree rotational symmetry (as does, of course, the set of cells containing odd numbers). For example, because the bottom left entry (4) is an even number, the top right entry must also be an even number.

Questions to consider: Suppose you color in all the odd entries in the completed puzzle above. How many such colorings are possible in a 9x9 Sudoku board? How many Sudoku boards are there that have parity symmetry? What about if instead of distinguishing mod 2 we consider mod 3? As always, we can also ask how many intial conditions are necessary to guarantee a unique solution; but in this case we can also ask about the minimum number of even conditions and the minimum number of odd conditions.
Solutions are due by noon on Tuesday, March 14, 2006.
Return solutions ON PAPER to Laura Taalman, Burruss 127, MSC 7803.
Include your name and email address with your solution.