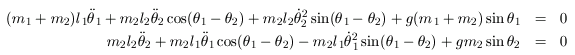We consider a double pendulum with two masses m₁ and m₂ connected by rigid (massless) wires of l₁ and l₂. As illustrated below, the angles formed by the wires are denoted by θ₁ and θ₂:

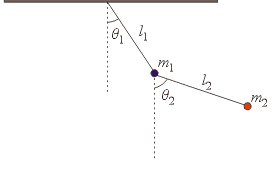
Letting the position of the two masses be denoted by (x₁, y₁) and (x₂, y₂) it is easy to see that:

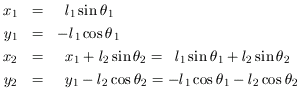
Now, letting g denote gravity, it follows that the potential energy is given by:

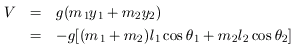
Further, letting v₁ and v₂ denote the velocities of m₁ and m₂ respectively, the kinetic energy is given by:

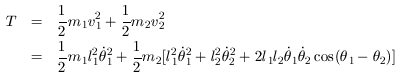
The difference between the total kinetic energy and the total potential energy, called the Lagrangian, is defined as L = T - V. Therefore:

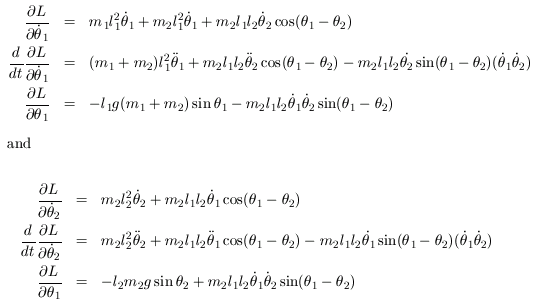
This leads to the following (Euler-Lagrange) differential equations: