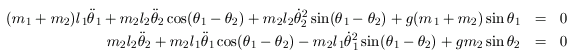We consider a double pendulum with two masses m1 and m2 connected by rigid (massless) wires of l1 and l2. As illustrated below, the angles formed by the wires are denoted by θ1 and θ2:

Letting the position of the two masses be denoted by (x1, y1) and (x2, y2) it is easy to see that:

Now, letting g denote gravity, it follows that the potential energy is given by:

Further, letting v1 and v2 denote the velocities of m1 and m2 respectively, the kinetic energy is given by:

The difference between the total kinetic energy and the total potential energy, called the Lagrangian, is defined as L = T - V. Therefore:

This leads to the following (Euler-Lagrange) differential equations: