Problem of the Week #3
Spring 2006:
Special All-Sudoku Semester
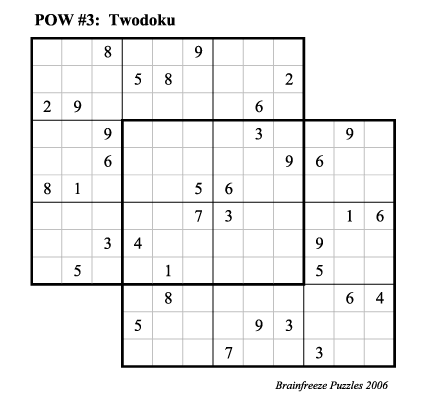
This week's Sudoku variation is to have two overlapping Sudoku boards.
Neither of the 9 x 9 boards has a unique solution on its own, but the
combined puzzle does have a unique solution. Sudoku puzzles with multiple
overlapping boards are common in British, Australian, and Japanese papers
and magazines. Probably the most common variation of this type is a
five-board variation known as "Samurai Sudoku". Our puzzle below has a
rather large four-block
region of overlap, which leads to some nice conditions on the
squares outside of the overlap. Double Sudoku puzzles like this one are
also sometimes contructed with two-block and one-block overlaps, which lead
to different solution strategies. Puzzles such as these place greater
restrictions on some cells, which can make solving the puzzle easier; but
on the other hand, the greater restrictions allow there to be fewer initial
conditions, which can make a puzzle more difficult.
Rules: Fill in the grid below so that each of the 9 x 9 squares is a
valid Sudoku puzzle. That is, fill in the grid so that
each row, each column, and each 3 x 3 block
contained within each of the two 9 x 9 grids contains each of the numbers
1, 2, ..., 9 exactly once.
As with any type of Sudoku puzzle, we could ask how many completed boards are
possible or how few initial conditions can lead to a unique solution.
Here is a research question that might not be too difficult: Given that
the number of 9 x 9 Sudoku boards is known (see the first
Problem of the Week),
how many Twodoku boards like the one above are possible?
Solutions are due by noon on Tuesday, January 31, 2006.
Return solutions ON PAPER to Laura Taalman, Burruss 127, MSC 7803.
Include your name and email address with your solution.

